背包问题贪心算法的证明

背包问题是一类经典的组合优化问题，涉及在给定容量的背包中选择一组物品放置以达到最大总价值。在解决背包问题时，贪心算法是一种常用的方法之一。贪心算法通过每次选择当前状态下最优的策略来逐步构建整体的最优解。下面将对背包问题的贪心算法进行证明。

假设有n个物品和一个容量为C的背包，每个物品i有一个重量wi和一个价值vi。我们要选择哪些物品放入背包中，使得在不超过背包容量的前提下，背包中物品的总价值最大化。

贪心算法基于一个关键观察：对于每个物品i，我们可以计算其单位重量的价值vi/wi。我们可以按照这个单位重量价值从大到小排序物品，并依次将单位重量价值最高的物品放入背包中，直到背包无法再容纳更多物品为止。

证明贪心算法的正确性可以通过反证法来进行。假设存在一个最优解不满足贪心选择策略，即存在一种更优解使得贪心选择策略无法得到最优解。

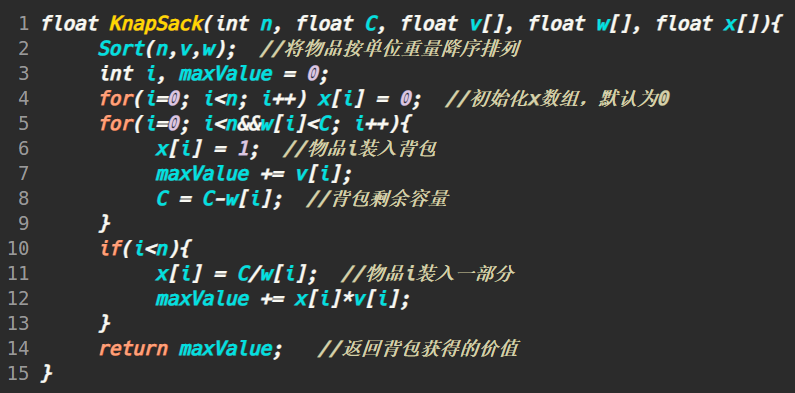
设最优解为S，贪心算法得到的解为G。假设在选择物品时，贪心算法先选择了物品k，而最优解S中并没有选择物品k。根据贪心算法的选择策略，我们可以得出vi/wi >= vk/wk，即物品k的单位重量价值不小于其他未选中的物品。